কেন্দ্রীয় প্রবণতার পরিমাপগুলি (Measures of Central Tendency) হলো এমন পরিসংখ্যানিক পরিমাপ যা একটি ডেটাসেটের কেন্দ্রীয় বা সাধারণ মান নির্দেশ করে। এটি ডেটাসেটের প্রধান বৈশিষ্ট্যগুলো বুঝতে সাহায্য করে এবং সাধারণত তিনটি গুরুত্বপূর্ণ পরিমাপ অন্তর্ভুক্ত করে:
গড় হলো ডেটাসেটের সব মানের যোগফলকে ডেটাসেটের মানের মোট সংখ্যায় ভাগ করে পাওয়া মান। এটি ডেটাসেটের কেন্দ্রীয় মানের একটি গুরুত্বপূর্ণ নির্দেশক।
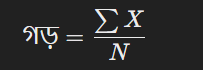
গণনা পদ্ধতি:
যেখানে:
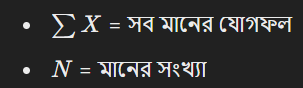
উদাহরণ:
ডেটাসেট: 5, 10, 15
গড়:
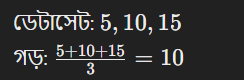
মধ্যক হলো ডেটাসেটের ক্রমানুসারে সাজানো মানগুলোর মধ্যে কেন্দ্রে থাকা মান। যদি ডেটাসেটের মোট মান বিজোড় হয়, তবে মধ্যক হবে একক একটি মান; আর জোড় হলে মাঝখানের দুইটি মানের গড় হবে মধ্যক।
উদাহরণ:
ডেটাসেট (বিজোড়): 3, 5, 7
মধ্যক: 5
ডেটাসেট (জোড়): 2, 4, 6, 8
মধ্যক:
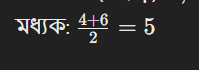
বহুলক হলো ডেটাসেটের মধ্যে সবচেয়ে বেশি সংখ্যক বার পুনরাবৃত্তি হওয়া মান। এটি বিশেষত সেই ক্ষেত্রে গুরুত্বপূর্ণ যেখানে ডেটাসেটের মধ্যে কিছু নির্দিষ্ট মান বেশি ঘটে।
উদাহরণ:
ডেটাসেট:2, 3, 3, 5, 7
বহুলক: 3
১. ডেটার সারাংশ দেওয়া: ডেটাসেটের মোট প্রবণতা বোঝায়।
২. তুলনামূলক বিশ্লেষণ: বিভিন্ন ডেটাসেটের মধ্যে তুলনা করতে সাহায্য করে।
৩. বিশ্লেষণ সহজ করা: গবেষণা ও পরিসংখ্যানে ডেটার বিশ্লেষণ সহজতর হয়।
কেন্দ্রীয় প্রবণতার পরিমাপ গড়, মধ্যক এবং বহুলকের মাধ্যমে ডেটাসেটের মৌলিক বৈশিষ্ট্য নির্ধারণ করতে সাহায্য করে। প্রতিটি পরিমাপ ভিন্ন ভিন্ন পরিস্থিতিতে কার্যকর।
Read more